The Hogwild! idea

Posted on by

the Diploma thesis learning – April 15, 2021

I have been working on a project based on the paper “HOGWILD!: A Lock-Free Approach to Parallelizing Stochastic Gradient Descent“.

https://papers.nips.cc/paper/2011/file/218a0aefd1d1a4be65601cc6ddc1520e-Paper.pdf

First iteration was reading the paper and preparing the logical model how Stochastic Gradient Descent, a.k.a. SGD, works and how it would be possible to paralelize.

Creating the Julia project

@everywhere function run_SSP_worker(batch, server, channel, model, ps, loss)
    id = myid()
    println("$(id) has started!")
    while fetch(channel) != nothing
        println("$(myid()) is bamboozled!")
        xs = take!(channel)
        println("$(myid()) has\n $(ps)\n $(xs)")
        data = batch()
        # WHY AM I NOT ALLOWED TO REMOVE MODEL HERE??
        gs = calculate_gradient(loss, model, ps, xs, data)
        information = Information(id, gs)
        println("$(data)\n # $(xs)\n # $(gs)")
        @sync put!(server, information)
    end
end

Math code is E=mc^2


At first, we sample f(x) in the N (N is odd) equidistant points around x^*:

    \[f_k = f(x_k),\: x_k = x^*+kh,\: k=-\frac{N-1}{2},\dots,\frac{N-1}{2}\]


where h is some step.
Then we interpolate points {(x_k,f_k)} by polynomial

(1)   \begin{equation*} P_{N-1}(x)=\sum_{j=0}^{N-1}{a_jx^j}\end{equation*}


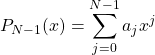
Its coefficients {a_j} are found as a solution of system of linear equations:

(2)   \begin{equation*} \left{ P_{N-1}(x_k) = f_k\right},\quad k=-\frac{N-1}{2},\dots,\frac{N-1}{2}\end{equation*}


Here are references to existing equations: (1), (2).
Here is reference to non-existing equation (??).